Project Overview

Asbestos is the name of a group of six different fibrous minerals: Chrysotile, amosite, crocidolite, tremolite, anthophyllite, and actinolite. Among these, Chrysotile or white asbestos is the most commonly type of asbestos and is found in roofs, ceilings, walls and floors of buildings. Amosite is used in cement sheet and pipe insulation, and found in insulating board, ceiling tiles, and thermal insulation products. Anthophyllite is found in composite flooring [1]. Exposure to asbestos may cause various diseases such as lung cancer, mesothelioma, asbestosis, pleural plaques, thickening, and effusion [2,3] as well as may lead to lagyngeal and some other cancers [4].

Recent years have seen the application of association rule analysis in point-of-sale data to find items that are frequently bought by customers to support marketing promotions, inventory management, and customer relationship management [9]. In this paper, we introduce the application of association rule analysis to text data in facilities management for asbestos presence. The usage of the technique as well as the results may help reduce the risk of asbestos exposure to facilities workers, help businesses lower the risk of lawsuits, help asbestos technicians in targeting the areas or materials that contain asbestos, and help management in setting priorities in asbestos assessments.

Association Rule Analysis

Data mining tasks include clustering, classification,  association rule analysis, and anomaly detection [9]. One of the most important data mining applications is association rules mining. Association rule analysis was first mentioned in 1993 [5-8], is used to identify relationships among a set of items in a database. These relationships are based on the co-occurrence of the items to find rules that predict the occurrence of some items based on the occurrences of other items through transactions in the database. Given a rule

                                        X -> Y                                                                                                                              (1)

in which X and Y are disjoint item sets, the support of the rule indicates the fraction of transactions that contain both X and Y, and is defined as follows [9,10]

                Support(X→Y) = P(X,Y)                                                                                                             (2)

The confidence measures how often items in Y appear in transactions that contain X, and is defined as follows [9,10]

               Confidence(X→Y) = P(X|Y)                                                                                                          (3)

The lift measures the dependency of X and Y on one another. The lift of 1 indicates the independency between X and Y. Higher lift implies more useful rules. The lift of a rule is defined as follows [9,10]

             Lift(X→Y)=(P(Y│X))/P(Y) =(P(X,Y))/(P(X)P(Y) )                                                                                          (4)

Data Pre-processing and Modeling

Assessment data were collected by ATC Associates for 295 buildings owned by the State of Connecticut. A C# application was developed that was able to read and convert various free-style spreadsheets into the record data type. Original assessment data in Excel spreadsheets were then read into an Oracle database and stored as a table. There are 295 assessments, each for 1 building. Each assessment in the form of an Excel spreadsheet contains of multiple material items in various locations in the corresponding building. The total of rows are 220532 with different types of data. The 2 fields selected for modeling are the material description and the asbestos content (containing descriptions for chrysotile, amosite, anthophyllite, actinolite, tremolite, and crocidolite). Both fields are in the free-text form. The model was developed in R, and connected directly to the Oracle database using an ODBC connection. Fig. 1 shows an excerpt of the data with 2 free-text fields. The free text fields contain both upper-case and lower-case letters, numbers, special characters, abbreviation, etc. and need to be pre-processed.

In the pre-processing stage, abbreviated names of asbestos were fixed using regular expressions, then the 2 text fields were merged as the source for text mining. White spaces, numbers, punctuations, stop words were removed. All the text data were converted to the lower case. A binary document-term matrix is formed to serve the association rule mining. The columns are the presence of words with values of 0 or 1 from 2 merged fields after processing; the rows are that from the assessment data table.

Fig. 1 An excerpt of the data set

Results

Mined rules are filtered to display rules with asbestos on the right side of the rules. With minimal support and minimal confidence set to 0.0001, and 0.01, respectively, the number of mined association rules containing “chrysotile” on the right side of the rule (consequent) is 112. Fig. 2 shows 20 rules for “chrysotile” on the consequent. In each row, the first number is the rule number, then the antecedent and consequent, support, confidence, and lift. Low support indicates the expected low presence of asbestos in the assessed materials. The presence of chrysotile is often found in materials with words in the item set on the left side. The high values of lift >100 indicate the dependency of chrysotile presence on the set of words in the antecedent. Materials containing {dotted}, {dotted, floor}, {dotted, tile}, {linoleum, squares}, {squares, yellow}, {dotted, floor, tile}, {linoleum, squares, yellow}, {associated, floor, green}, {associated, floor, green, mastic}, {ceiling, compound, joint} in the material description surely contain chrysotile. Rules 7 and 9 can be combined using word stemming. Rules 4 and 14 can be combined using word stemming as well. Rules after 11 have slightly lower confidence.

Notice that the 20^th rule contains “amosite”, another type of asbestos, in the antecedent. This rule may be useful for testing the presence of chrysotile given that amosite is present and the materials contain “insulation”. It can be seen that the confidence is high (86.3%); the lift is high (109.27) indicating the usefulness of the rule.

1 {dotted} => {chrysotile} 0.0001269657 1.00000000 126.597015 2 {dotted,  floor} => {chrysotile} 0.0001269657 1.00000000 126.597015 3 {dotted,  tile} => {chrysotile} 0.0001088277 1.00000000 126.597015 4 {linoleum,  squares} => {chrysotile} 0.0001995175 1.00000000 126.597015 5 {squares,  yellow} => {chrysotile} 0.0001133622 1.00000000 126.597015 6 {dotted,  floor,  tile} => {chrysotile} 0.0001088277 1.00000000 126.597015 7 {linoleum,  squares,  yellow} => {chrysotile} 0.0001133622 1.00000000 126.597015 8 {associated,  floor,  green} => {chrysotile} 0.0001405692 1.00000000 126.597015 9 {linoleum,  square,  yellow} => {chrysotile} 0.0001859141 1.00000000 126.597015 10 {ceiling,  compound,  joint} => {chrysotile} 0.0002176555 1.00000000 126.597015 11 {associated,  floor,  green,  mastic} => {chrysotile} 0.0001405692 1.00000000 126.597015 12 {associated,  green} => {chrysotile} 0.0001405692 0.96875000 122.640858 13 {associated,  green,  mastic} => {chrysotile} 0.0001405692 0.96875000 122.640858 14 {linoleum, square} => {chrysotile} 0.0002766038 0.96825397 122.578062 15 {linoleum,  pattern} => {chrysotile} 0.0001269657 0.96551724 122.231601 16 {square,  yellow} => {chrysotile} 0.0001859141 0.95348837 120.708782 17 {green,  linoleum} => {chrysotile} 0.0001587071 0.94594595 119.753933 18 {tan,  tiles} => {chrysotile} 0.0001269657 0.93333333 118.157214 19 {floor,  tan,  tiles} => {chrysotile} 0.0001269657 0.93333333 118.157214 20 {amosite,  insulation} => {chrysotile} 0.0003718281 0.86315789 109.273213

Fig. 2 Rules containing “chrysotile” in the consequent

Fig. 3 shows the scatter plot of the 112 rules containing “chrysotile” in the consequent. Notice that rules with lower confidence have lower lift. Rules with high confidence have low support. This behavior is expected in the case of asbestos-containing materials.

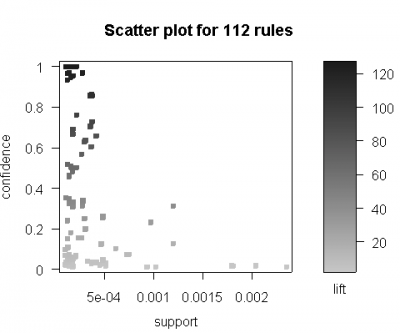
Fig. 3 Scatter plot for 112 rules rules containing “chrysotile” in the consequent

1 {chrysotile, insulation, pipe} => {amosite} 0.0003536902 0.57352941 1303.93390 2 {chrysotile, insulation} => {amosite} 0.0003718281 0.49696970 1129.87341 3 {chrysotile, pipe} => {amosite} 0.0003536902 0.48750000 1108.34381

Fig. 4 displays 3 rules for “amosite” in the consequent with considerable confidence. The confidence is approximately 57.35%, 49.70% and 48.75%, respectively. The lift is high for all the 3 rules. Notice that the left side of the rules contain “chrysotile”. Given that chrysotile is present and the materials contain “pipe”, or “insulation”, or both, the probabilities of found amosite (P({chrysotile, pipe}|{amosite}), P({chrysotile, insulation, pipe}|{amosite}), and P({chrysotile, insulation}|{amosite})) are 57.35%, 49.70% and 48.75%. Asbestos technicians may need to test for chrysotile given that the related materials contain amosite.

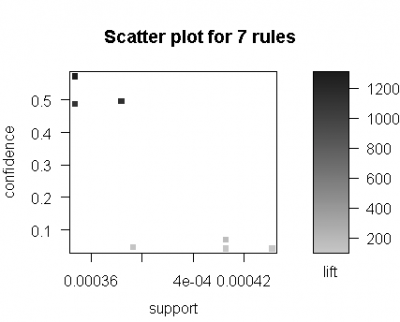
Fig. 5 Scatter plot of 7 rules containing “amosite” in the consequent

The scatter plot in Fig. 5 shows the 7 mined rules containing “amosite” in the consequent. The behavior that the 3 rules with considerable confidence are with low support can be observed again in the case of amosite.

Fig. 6 provides 3 rules for “anthophyllite” in the consequent. The confidence is much low for these rules, and it is much lower for the next rules. The confidence is even significantly lower for other types of asbestos which have not been discussed above so the results are not presented.

1 {base, black, mastic} => {anthophyllite} 0.0002403279 0.105577689 280.521192 2 {base, black, cove, mastic} => {anthophyllite} 0.0002403279 0.105577689 280.521192 3 {black, cove, mastic} => {anthophyllite} 0.0002403279 0.105367793 279.963496

Fig. 6 Rules containing anthophyllite in the consequent

In the project, we have applied text mining and association rule analysis with asbestos assessment data. The technique as well as the results can be used in various aspects in facilities management, such as prioritizing asbestos assessment tasks, serving as the additional layer of protection for facilities workers, helping management in decision support, and supporting asbestos technicians in narrowing the asbestos-containing materials and locations. The research can be extended toward finding association rules for asbestos between adjacent locations (attic, stairs, rooms above and below, rooms surround, etc.), finding sequences of asbestos removals in combination with other data.

References

• Type of asbestos [Online]. Available: http://www.asbestos.com/asbestos/types.php (Accessed: 6/1/2015)
• Environmental Health Criteria 203: Chrysotile asbestos. Geneva, World Health Organization, 1998
• Environmental Health Criteria 53: Asbestos and other natural mineral fibres. Geneva, World Health Organization, 1986
• Committee on Asbestos: Selected Health Effects, Board on Population Health and Public Health Practices. Asbestos: Selected cancers. Washington D.C., The National Academy Press, 2006
• Agrawal, T. Imielinski, and A.N. Swami, Mining Association Rules Between Sets of Items in Large Databases, Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, pp. 207-216, Washington, D.C., May 1993.
• C. Aggarwal, Z. Sun, and P. S. Yu, “Online Algorithms for Finding Profile Association Rules”, Proceedings of the ACM CIKM Conference, 1998, pp 86-95.
• C. Aggarwal, J. L. Wolf, P. S. Yu, and M. Epelman, “Online Generation of Profile Association Rules”, Proceedings of the International conference on Knowledge Discovery and Data Mining, August 1998.
• C. Aggarwal, and P. S. Yu, “A New Framework for Itemset Generation”, Principles of Database Systems (PODS) 1998, Seattle, WA
• Tan, M. Steinbach, and V. Kumar, Introduction to Data Mining, Addison Wesley, 2005
• Han, M. Kamber, J. Pei, Data Mining : Concepts and Techniques: Concepts and Techniques (3rd Edition), Morgan Kaufmann, 2011